Teaching AI to Think Like Algorithms
Neural Algorithmic Reasoning.
Why Neural Algorithmic Reasoning?
Traditional algorithms are deterministic but struggle with unstructured or noisy data. Neural networks (NNs), on the other hand, learn from data but often behave like black boxes with little interpretability.
Neural Algorithmic Reasoning (NAR) bridges this gap by embedding algorithmic logic into neural networks, combining the best of both worlds: structured reasoning and adaptability.
How We Built It
1. Encoding Graph Data
Using PyTorch, we transformed raw graphs into numerical embeddings:
- Input: Adjacency matrices or edge lists.
- Output: Vector representations preserving graph structure.
2. Processing with a Neural Network
We used a Message-Passing Neural Network (MPNN) to simulate BFS traversal:
- Step 1: Nodes exchange information with neighbors.
- Step 2: Messages are aggregated (e.g., max pooling).
- Step 3: Node states update iteratively, mirroring BFS layers.
3. Decoding the Output
After processing, we extracted two key predictions:
- Parent Nodes: "Which node discovered me?"
- Reachability: "Is this node connected to the source?"
To evaluate how well our model understood algorithmic reasoning, we needed a structured and interpretable benchmark. Breadth-First Search (BFS) was the perfect candidate.
Why Breadth-First Search?
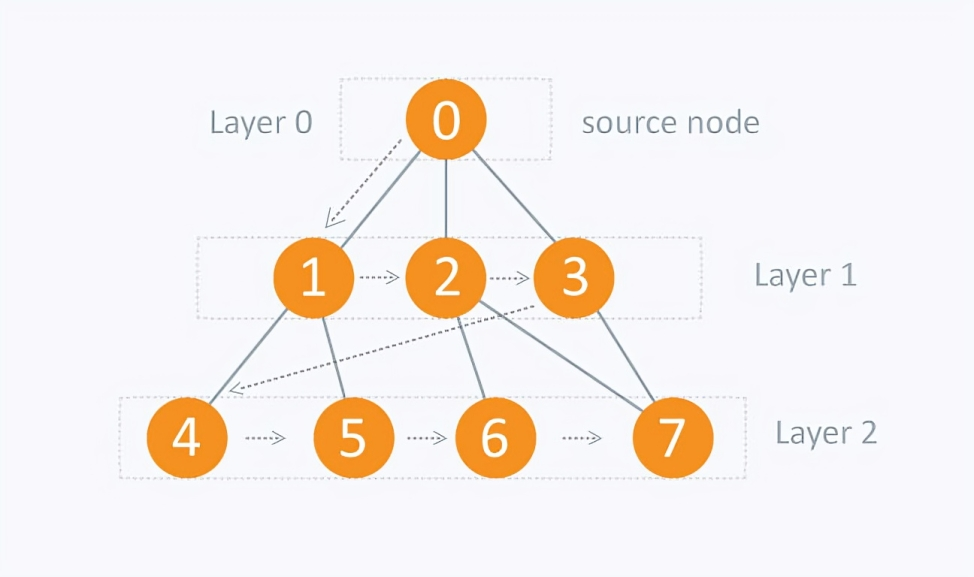
Breadth-First Search (BFS) is a fundamental graph traversal algorithm used to explore a graph or tree systematically, layer by layer. It is widely used in computer science and artificial intelligence due to its completeness and optimality in unweighted graphs.
Key Characteristics of BFS:
- Exploration Order: Visits all nodes at the current depth before proceeding to the next depth level.
- Data Structure:
O(V + E), where (V) is the number of vertices and (E) is the number of edges. - Optimality: Guarantees the shortest path in unweighted graphs.
- Completeness: Always finds a solution if one exists in a finite graph.
Applications of BFS:
- Shortest Path Finding in unweighted graphs (e.g., Dijkstra’s algorithm without weights).
- Network Traversal (e.g., social networks, web crawling).
- AI & Game Development (e.g., pathfinding algorithms).
Benchmarking & Generalization:
Understanding BFS not just in terms of its final outputs but also its step-by-step execution serves as a strong benchmark for evaluating generalization in learning models. Since BFS follows a well-defined and predictable sequence of operations, mastering its process can indicate deeper comprehension of algorithmic reasoning.
Training and Optimization
Key Techniques
- Loss Function: Penalizes errors in both final outputs and intermediate steps.
- Datasets:
- Training: 400 Erdős–Rényi graphs (20–100 nodes, random edges).
- Out-of-Distribution (OOD) Testing:
- Larger Erdős–Rényi graphs (up to 3,000 nodes).
- Barabási–Albert graphs (with "rich-get-richer" connectivity).
How Well Did It Work?
Performance on Training Data
| Metric | Accuracy | Interpretation |
|---|---|---|
| Edge Prediction | 97.11% | Learned graph connectivity. |
| Parent Nodes | 97.36% | Reconstructed BFS tree. |
| Reachability | 95.4% | Identified connected components. |
Out-of-Distribution Generalization
| Graph Type | Nodes | Edge Accuracy | Parent Accuracy | Reach Accuracy |
|---|---|---|---|---|
| Erdős–Rényi | 3,000 | 99.32% | 99.97% | 100% |
| Barabási–Albert | 3,000 | 98.94% | 99.70% | 99.89% |
Key Takeaways
- Scalability: Model accuracy improved with graph size, indicating it inferred BFS principles rather than memorizing data.
- Robustness: Performed well on Barabási–Albert graphs despite training only on random graphs.
What’s Next?
Expanding to Complex Algorithms
- Test on recursion, dynamic programming, and combinatorial optimization problems.
Real-World Applications
- Network Analysis: Identify key nodes in critical infrastructure.
- Robotics & Pathfinding: Improve autonomous navigation systems.
- Hybrid AI Systems: Combine NAR with reinforcement learning (RL) for adaptive decision-making.
Final Thoughts
This project demonstrates that neural networks can learn to approximate algorithmic logic, achieving strong performance in mimicking BFS even on graphs significantly larger than those seen during training. While there is still much to explore, these results highlight the potential of AI systems that incorporate both structured reasoning and adaptability.
Want to explore further? Check out our implementation: GitHub Repository